시뮬레이션으로 기계제품의 진동(vibration), 안전성(safety), 내구성(durability) 등을 평가할 수 있습니다. 시뮬레이션은 결과가 실제와 얼마나 비슷한 지 비교해서 평가할 수 있습니다. 그래서 시뮬레이션으로 계산한 값과 센서를 사용해서 계측한 값을 비교합니다. 시뮬레이션 결과와 계측을 비교할 때 대표적으로 사용하는 것이 응력(stress)입니다. 계측에서는스트레인 게이지를 사용해서 변형량을 측정하고 응력을 계산합니다. 시뮬레이션에서는 유연체를 사용해서 응력을 계산합니다. 이 글에서 사용한 리커다인(RecurDyn) 시뮬레이션 소프트웨어는 FFlex와 RFlex에서 유연체를 제공합니다. ‘Flex’는 ‘Flexible’의 줄임말입니다. ‘Flexible’은 유연함을 뜻합니다. 원래 많은 기계부품(금속)은 유연합니다. 여기서 유연하다는 것은 힘을 받으면 모양이 변한다는 것입니다. 활을 예로 생각해 볼 수 있습니다. 활 시위를 당기면 활의 모양이 변했다가 다시 원래 모양으로 돌아오는 것이 대표적인 예입니다. 시뮬레이션에서 유연함을 고려하면 그렇지 않은 경우보다 계산이 복잡해지고, 시간이 많이 소요됩니다. 그래서 많은 경우 계산의 목적과 효율성을 고려해서 물체가 ‘유연하지 않다’고 가정하고 계산을 합니다. 어떤 물체가 ‘유연하지 않다’고 가정하면 그 물체를 강체(rigid body, 刚体)라고 합니다. 강체는 형상이 전혀 변하지 않는다고 가정하기에 계산이 쉽습니다. 반대로 유연한 상태 그대로의 물체를 유연체(flexible body, 柔体)라고 합니다. 많은 경우, 강체로 가정을 하고 시뮬레이션을 해도 필요한 결과를 얻을 수 있습니다. 하지만 형상의 변화가 결과에 영향을 미친다거나, 물체에 발생하는 응력이 필요하다면, 유연체로 가정하고 시뮬레이션을 할 필요가 있습니다. 일반적으로 유연체를 많이 사용할수록 시뮬레이션 품질이 좋아진다고 할 수 있습니다. 하지만 그만큼 계산량이 많아 집니다. 그래서 계산 결과를 얻기까지 시간이 오래 걸립니다. 시뮬레이션에서 유연체를 사용하는 방법에는 2가지가 있습니다. 촘촘하게 풀지만 시간과 자원을 많이 사용하는 방법과, 이에 비해 느슨하게 풀지만 시간과 자원을 적게 쓰는 방법입니다. 첫번째 방법의 사용 범위가 두번째 방법에 비해서 넓습니다. 이를테면 첫번째 방법은 선형, 비선형에서 모두 사용하지만, 두번째 방법은 선형에서만 사용합니다.

이렇게 보면 촘촘하게 푸는 방법을 대부분의 경우에 사용하면 될 것 같습니다. 하지만 실제로 어느 것을 더 많이 사용한다고 말하기 어렵습니다. 왜냐하면 제품의 변형이 적거나 진동을 평가하는 것이 목적일 때는 느슨하게 푸는 방법이 주는 결과값도 품질이 좋으면서 계산 시간이 더 짧은 경우가 많기 때문입니다. 리커다인에서는 FFlex(에프플렉스)가 촘촘하게 푸는 방법에 해당하고 RFlex(알플렉스)가 느슨하게 푸는 방법에 해당합니다. FFlex는 Full Flexible Body를, RFlex는 Reduced Flexible Body를 뜻합니다. 여기에서는 편의상 ‘전체를 사용하는 방법’과 ‘줄여서 사용하는 방법’이라고 하겠습니다. 리커다인과 같이 기계가 움직이는 완제품 또는 반제품 상태를 시뮬레이션 하는 프로그램에서는 유연체를 고려하기 위해 ‘줄여서 사용하는 방법’을 먼저 채택했습니다. 왜냐하면 ‘전체를 사용하는 방법’을 제품이 움직이는것과 동시에 계산하기 위해서는 매우 복잡한 수학적인 난제가 있었기 때문입니다. 이 글에서는 ‘줄여서 사용하는 방법’을 알아보겠습니다.

우리가 유연체를 사용한 시뮬레이션에서 확인하는 것으로 응력(stress)이 있습니다. 응력은 탄성계수(재료상수)에 변형률을 곱해서 얻습니다. 변형률은 원래 길이와 변형량의 차이를 비율로 나타낸 것입니다. 결과적으로 변형량을 알면 응력을 구할 수 있습니다. 실제로 사용하는 용어는 아니지만, 편의상 변형량을 계산할 수 있는 곳을 ‘변형점’이라고 하겠습니다. 부품을 유연체로 만드는 방법은 부품에 변형점을 배치하는 것입니다. 이 때 변형점을 많이 사용하면 유연체가 실제 부품과 더 비슷해지는 장점이 있습니다. 하지만 변형점을 많이 사용할 수록 컴퓨터 자원을 많이 사용하고, 결과를 얻기까지 시간이 길어지게 되는 단점이 커집니다.

변형점의 개수가 많아 지는 것 만으로도 계산 시간이 길어지는데, 여기에 제품이 동작하는 것까지 같이 고려한다면 필요한 시간은 더 길어 집니다. 그래서 변형점 전부를 사용하는 방법 대신 ‘줄여서 사용하는 방법’을 먼저 선택해서 사용하게 되었습니다. 방법을 설명에 앞서 비슷한 수학 개념 하나를 먼저 설명하겠습니다. 프랑스의 수리물리학자 푸리에(Fourier)는 “복잡한 하나의 파동은 실은 단순한 파동이 몇 개나 더해진 것”이라고 했습니다. 이 말은 아무리 복잡한 파동도 단순한 파동 여러 개로 분리할 수 있고, 이 단순한 파동들을 더하기만 하면 복잡한 파동과 같아진다는 뜻입이다. 아래 그림은 복잡한 파동 (C)가 단순한 파동 (A)와 (B)로 분리될 수 있음을 보여줍니다.

이미치 출처: 책 <수학으로 배우는 파동의 법칙> 저자: Transnational College of LEX

어떤 복잡한 진동도 단순한 진동 여러 개로 분리할 수 있고, 다시 이 단순한 진동 여러 개를 더해서 어떤 복잡한 진동도 표현할 수 있다는 뜻입니다. 복잡한 기계 진동도 단순한 진동 여러 개로 분리할 수 있습니다.

기계 진동에서는 고유모드(고유진동)가 단순한 진동입니다. 물체는 무한개의 고유모드를 가집니다. 이 중 몇 개의 고유모드를 선택해서 더하는 것 만으로 복잡한 진동을 포함한 대부분의 기계 진동을 표현할 수 있습니다.

고유모드의 주파수를 고유진동수(고유주파수, Natural frequency)라고 합니다. 외부에서 들어오는 하중의 주파수가 물체의 고유진동수에 가까워지면 물체가 진동하는 변형량이 매우 커집니다. 의도하지 않은 진동이 과하게 커지는 것은 문제를 일으킵니다. 특별히 고유진동수와 외부 하중의 주파수가 같아지면 이를 공진(Resonance, 공명)이라고 합니다. 아래 동영상은 길이가 다른 두 금속 막대가 다른 주파수에서 공진하는 것을 보여줍니다. 설계에서 의도하지 않은 공진은 피해야 합니다.

물체의 고유진동수는 시험(계측) 또는 계산을 통해서 구할 수 있습니다. 먼저 시험을 통해서 어떻게 구하는지 살펴보겠습니다. 이 글에서 시험을 통해서 고유진동수를 구하는 이유는 나중에 계산을 통해서 얻은 값과 이 값을 비교하여 시뮬레이션 결과가 얼마나 정확한지 판단하기 위해서입니다. 고유진동수는 임팩 해머(Impact hammer) 시험으로 얻을 수 있습니다. 어떤 물체에 가속도 센서를 부착하고 진동이 없는 상태에서 임팩 해머로 충격합니다. 진동이 사라질 때까지 가속도 변화를 측정합니다. 여기서 가속도는 진동합니다. 계측한 진동 신호는 여러 모드로 분리할 수 있음을 앞에서 설명했습니다. 이 때 사용하는 방법이 고속 푸리에 변환(FFT, Fast Fourier Transform)입니다. 가속도 신호를 FFT하면 신호를 구성하고 있는 고유진동수를 알 수 있습니다. 다음 동영상은 높이가 다른 3개의 금속막대의 고유진동수를 측정한 시험입니다

위 영상에서 측정에 사용한 금속막대의 재질은 철(steel)이며 크기는 각각 3x50x500, 5x50x500, 10x50x500 mm입니다. 측정된 고유진동수는 다음과 같습니다.

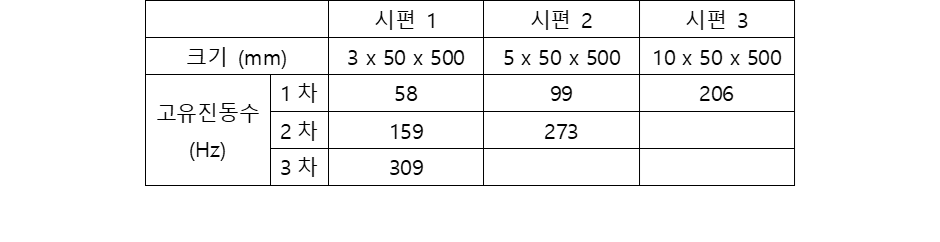
시뮬레이션(계산)으로 고유진동수를 얻는 방법이 ‘모드해석’입니다. 모드해석은 구조물의 고유진동수와 모드 형상(Mode shape)을 알아보는 해석입니다. 계산 방법은 선형대수학(Linear algebra)의 고유치 문제(Eigenvalue problem)를 푸는 방법과 동일합니다. 고유치 문제를 풀면 고유치(Eigen value)와 고유치 벡터(Eigen vector)를 얻습니다. 고유치 벡터와 모드 형상은 같은 말입니다. 고유치와 고유 진동수도 같은 말입니다. 모드해석(Modal analysis)은 Eigenvalue analysis라고도 합니다.

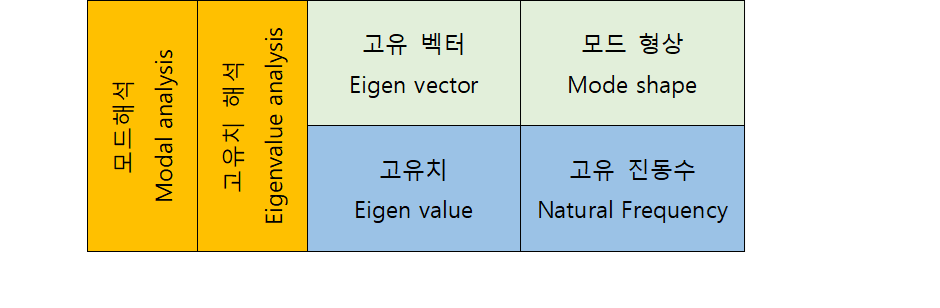
모드는 독립적입니다. 즉, 어느 고유 모드도 다른 고유모드들의 합성으로 만들어 질 수 없습니다. 반면에 구조물의 임의의 진동 형상은 모드의 합성으로부터 구할 수 있습니다. 이는 앞에서 프랑스 수리물리학자 푸리에가 아무리 복잡한 파동도 단순한 파동 여러 개로 분리할 수 있고 이 단순한 파동들을 더하기만 하면 복잡한 파동과 같아진다고 한 것과 같습니다. 즉, 서로 독립인 모드를 구하고, 이들을 합성해서 구조물의 진동을 표현할 수 있습니다. 아래 그림과 표는 위에서 소개한 시편 실험의 시뮬레이션과 계측의 오차를 보여줍니다.

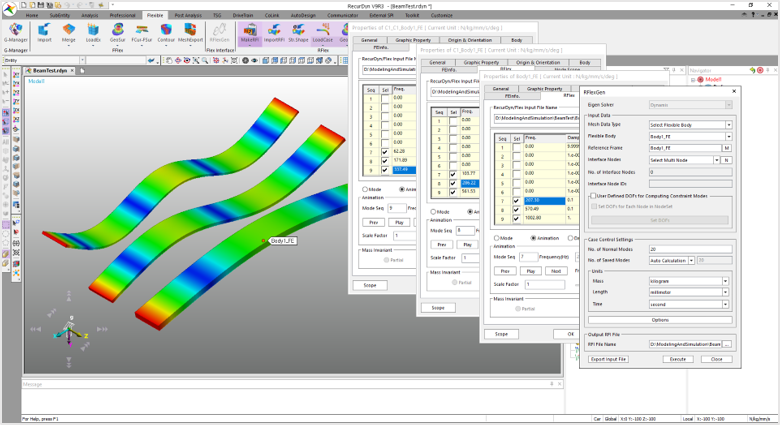
우리가 원하는 결과값이 응력인 경우가 많습니다. 모드 해석 결과를 사용해서 응력을 계산할 때 모드 형상을 이용합니다. 리커다인에서는 RFlex에서 이 방법을 제공합니다. RFlex에서 얻은 응력은 구조물의 진동과 안정성(safety) 과 내구성(durability) 평가에 사용할 수 있습니다.

참고)

이 글의 목적은 주제와 관련된 내용을 쉽게 훑고 넘어갈 수 있게 하는 것과, 개념을 파악하는데 필요한 지식을 소개하고, 연결시켜 주는 데 있습니다. (경우에 따라서는 정확하기보다는 이해를 돕기 위해 다소 변형된 설명이 있을 수도 있습니다.) 이 글을 읽고 개략적인 개념을 이해하고, 추가로 필요한 내용이 무엇인지를 알고 그것을 찾아보고 싶은 마음이 들었다면 저자의 목적을 달성한 것입니다. 따라서 본문에서 자세한 수식이나 이론, 전문용어의 사용은 가급적 줄였습니다. 다만 조금 더 설명이 필요한 부분은 아래에 추가했습니다.

1. 유한요소법에서 말하는 동적해석(Dynamic Analysis)과 ‘다물체 동역학’(MBD, Multi Body Dynamics)이 구별없이 사용되는 경우가 꽤 있습니다. 유한요소법에서는 진동(모드 해석)을 동역학의 범주로 넣기도 합니다. 지금까지 설명한 모드 해석도 유한요소법에서는 동적해석에 포함됩니다. 유한요소에서 말하는 동적해석은 모드 해석을 포함해서 조화응답 해석, 강제진동 해석, 스펙트럼 해석을 말합니다. 유한요소법에서 정적해석(Static analysis)은 계산에 강성(stiffness)을 사용합니다. 하지만 동적해석에서는 강성과 더불어 질량(mass)과 감쇠(damping)를 추가로 사용합니다. 질량과 감쇠를 계산에 사용하는 것을 동역학 또는 동해석이라고 한다고 보면 될 것 같습니다. 누군가 ‘동해석’ 또는 동역학 해석이라고 말했다면 이는 모드 해석, 조화응답 해석, 강제진동 해석, 스펙트럼 해석, 과도 해석(Transient Analysis) 등을 말하는 것으로 생각하면 될 것 같습니다. 다물체 동역학은 과도 해석에 속한다고 볼 수 있겠습니다.

2. 구조물이 갖는 고유진동수의 개수는 무한합니다. 유연체를 표현하기 위해 생성하는 변형점을 유한요소법(FEM, Finite Element Method)에서는 메쉬, 또는 격자라고 합니다. 유한요소법을 사용하면 격자 생성 단계에서 노드 개수가 결정이 됩니다. 동시에 모드 해석을 통해서 구해지는 고유진동수의 개수도 무한한 것에서 유한하게 결정이 됩니다.

3. 동적 해석(동역학)은 유한요소법과 함께 발전하고있습니다. 일례로 동적 해석도 주파수 및 응답 해석에서 유연체의 자유도(Degree of freedom) 수를 줄이는 축소모델링(ROM, Reduced order modeling)으로 발전했습니다. 자유도를 줄이면 계산에 필요한 컴퓨터 자원과 해석 시간을 줄일 수 있기 때문입니다. 조금 더 자세한 내용으로 들어가면 대표적인 것이 CMS(Component mode synthesis)입니다. CMS는 많은 자유도를 가진 substructure를 상대적으로 적은 수의 constraint 모드와 component 모드로 합성해서 대체하는 것입니다. CMS를 하는 방법에는 Craig-Bampton를 포함하여 여러가지가 있습니다. CMS는 모드 합성법(Modal synthesis), substructure synthesis, dynamic substructuring이라고 합니다. 이 글에서는 이해에 필요한 핵심 사항만 언급했지만, 리커다인의 RFlexGen에서 사용하는 방법도 CMS입니다.

4. 참고 문서: ‘Concepts and applications of finite element analysis’ 저자 Robert D. Cook 외